图的遍历
对无序图进行遍历,图记录在一个邻接矩阵中
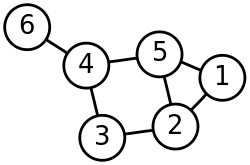
深搜算法:使用函数递归遍历一个节点中所有未达的邻接节点,结束返回上一层
广搜算法:借助辅助对列
伪码如下:
queue.push(start_node)
node[start_node]=used;
while(!queue.empty())
{
tmp_node=queue.pop()
foreach(n in node)
{
if(node[n]!=used&&tmp_node linked n)
{
queue.push(n)
node[n]=used
}
}
}
#include <iostream>
#include <cstdio>
#include <vector>
#include <list>
#include <string>
void print_reslut(
std::list<int>& node_vist_list,
std::list<std::string>& edges)
{
//print node list
while(!node_vist_list.empty())
{
std::cout << node_vist_list.front();
node_vist_list.pop_front();
}
std::cout << std::endl;
//print edges
while(!edges.empty())
{
std::cout << edges.front() << std::endl;
edges.pop_front();
}
}
template<int N>
int BFS(
int graph[N][N],
std::list<int>& node_vist_list,
std::list<std::string>& edges)
{
int node[N]={0};
std::list<int> tree_stack;
node_vist_list.clear();
edges.clear();
node[0] = 1;
tree_stack.push_back(0);
node_vist_list.push_back(0);
while(!tree_stack.empty())
{
int tmp_node = tree_stack.front();
tree_stack.pop_front();
for(int i=0;i<N;i++)
{
if(node[i]==0&&graph[tmp_node][i]==1)
{
tree_stack.push_back(i);
node[i]=1;
node_vist_list.push_back(i);
char e_str[256];
sprintf(e_str, "%d-%d", tmp_node, i);
edges.push_back(e_str);
}
}
}
return 0;
}
template<int N>
int DFS_reseve(
int graph[N][N],
std::list<int>& node_vist_list,
std::list<std::string>& edges,
int tmp_node,
int *node)
{
for(int i=0;i<N;i++)
{
if(node[i]==0&&graph[tmp_node][i]==1)
{
node[i] = 1;
node_vist_list.push_back(i);
char e_str[256];
sprintf(e_str, "%d-%d", tmp_node, i);
edges.push_back(e_str);
DFS_reseve(graph, node_vist_list, edges, i, node);
}
}
return 0;
}
template<int N>
int DFS(
int graph[N][N],
std::list<int>& node_vist_list,
std::list<std::string>& edges)
{
int node[N]={0};
std::list<int> tree_stack;
node_vist_list.clear();
edges.clear();
node[0] = 1;
tree_stack.push_back(0);
node_vist_list.push_back(0);
DFS_reseve(graph, node_vist_list, edges, 0, node);
return 0;
}
int main()
{
int graph_arr[6][6]={
{0,1,0,0,1,0},
{1,0,1,0,1,0},
{0,1,0,1,0,1},
{0,0,1,0,1,1},
{1,1,0,1,0,1},
{0,0,0,1,1,0}
};
std::list<int> node_vist_list;
std::list<std::string> edges;
std::cout << "BFS:" << std::endl;
BFS(graph_arr, node_vist_list, edges);
print_reslut(node_vist_list, edges);
std::cout << "DFS:" << std::endl;
DFS(graph_arr, node_vist_list, edges);
print_reslut(node_vist_list, edges);
return 0;
}