二叉树构造前中后序遍历
###定义
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
树和二叉树的三个主要差别: 1.树的结点个数至少为1,而二叉树的结点个数可以为0; 2.树中结点的最大度数没有限制,而二叉树结点的最大度数为2; 3.树的结点无左、右之分,而二叉树的结点有左、右之分。
完全二叉树和满二叉树 1.满二叉树:一棵深度为k,且有2^k-1个节点成为满二叉树 2.完全二叉树:深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中序号为1至n的节点对应时,称之为完全二叉树
###二叉树的遍历
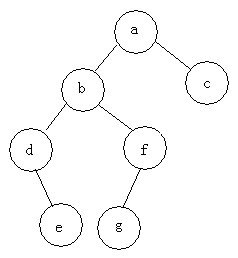
遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历,中序遍历,后序遍历。
1.前序遍历:根节点->左子树->右子树
2.中序遍历:左子树->根节点->右子树
3.后序遍历:左子树->右子树->根节点
#include <iostream>
#include <iterator>
#include <vector>
#include <algorithm>
#include <sstream>
template <typename Ty>
class BinarytreeNode
{
public:
BinarytreeNode():_data(),_lc(NULL),_rc(NULL){}
BinarytreeNode(const Ty& t):_data(t),_lc(NULL),_rc(NULL){}
BinarytreeNode(const Ty& t,BinarytreeNode* lc,BinarytreeNode* rc):_data(t),_lc(lc),_rc(rc){}
bool operator < (const BinarytreeNode& rhs)
{
return this->_data < rhs;
}
void setLeftchild(BinarytreeNode* lc)
{
this->_lc = lc;
}
void setRightchild(BinarytreeNode* rc)
{
this->_rc = rc;
}
void setData(const Ty& t)
{
this->_data = t;
}
Ty getData() const
{
return _data;
}
const BinarytreeNode<Ty>* getLeftchild() const
{
return _lc;
}
const BinarytreeNode<Ty>* getRightchild() const
{
return _rc;
}
BinarytreeNode<Ty>* getLeftchild()
{
return _lc;
}
BinarytreeNode<Ty>* getRightchild()
{
return _rc;
}
private:
Ty _data;
BinarytreeNode<Ty>* _lc;
BinarytreeNode<Ty>* _rc;
};
template <typename Ty, typename Iterator>
class Binarytree
{
public:
Binarytree(
Iterator pre_begin,
Iterator pre_end,
Iterator mid_begin,
Iterator mid_end)
{
root = new BinarytreeNode<Ty>();
if (!buildBinarytree(pre_begin, pre_end, mid_begin, mid_end, root))
{
std::cout << "prase tree error! please check input!" << std::endl;
delete root;
root = NULL;
}
}
~Binarytree()
{
if(root)
{
disposeNode(root);
root = NULL;
}
}
void printBinarytree(int type, std::ostream& ost = std::cout) const
{
printNode(root, type, ost);
ost << std::endl;
}
protected:
bool buildBinarytree(
Iterator pre_begin,
Iterator pre_end,
Iterator mid_begin,
Iterator mid_end,
BinarytreeNode<Ty>* p_node)
{
Ty mid_value = *pre_begin;
p_node->setData(mid_value);
int pre_len = 0;
Iterator tmp = mid_begin;
Iterator pre_it = pre_begin;
for(; tmp!=mid_end; tmp++,pre_it++)
{
if((*tmp) == mid_value)
{
break;
}
}
if((*tmp) != mid_value)
return false;
if (tmp != mid_begin)
{
BinarytreeNode<Ty>* lc = new BinarytreeNode<Ty>();
p_node->setLeftchild(lc);
if (!buildBinarytree(pre_begin+1, pre_it, mid_begin, tmp-1, lc))
{
delete lc;
return false;
}
}
else
{
p_node->setLeftchild(NULL);
}
if (tmp != mid_end)
{
BinarytreeNode<Ty>* rc = new BinarytreeNode<Ty>();
p_node->setRightchild(rc);
if (!buildBinarytree(pre_it+1, pre_end, tmp+1, mid_end, rc))
{
delete rc;
return false;
}
}
else
{
p_node->setRightchild(NULL);
}
return true;
}
void disposeNode(BinarytreeNode<Ty>* p_node)
{
BinarytreeNode<Ty> *lc = p_node->getLeftchild();
if (lc)
disposeNode(lc);
BinarytreeNode<Ty> *rc = p_node->getRightchild();
if (rc)
disposeNode(rc);
delete p_node;
}
void printNode(const BinarytreeNode<Ty> *p_node,int type, std::ostream& ost) const
{
if (type == 0)
{
ost << p_node->getData();
const BinarytreeNode<Ty> *lc = p_node->getLeftchild();
if (lc)
printNode(lc, type, ost);
const BinarytreeNode<Ty> *rc = p_node->getRightchild();
if (rc)
printNode(rc, type, ost);
}
else if (type == 1)
{
const BinarytreeNode<Ty> *lc = p_node->getLeftchild();
if (lc)
printNode(lc, type, ost);
ost << p_node->getData();
const BinarytreeNode<Ty> *rc = p_node->getRightchild();
if (rc)
printNode(rc, type, ost);
}
else if (type == 2)
{
const BinarytreeNode<Ty> *lc = p_node->getLeftchild();
if (lc)
printNode(lc, type, ost);
const BinarytreeNode<Ty> *rc = p_node->getRightchild();
if (rc)
printNode(rc, type, ost);
ost << p_node->getData();
}
}
private:
Binarytree(const Binarytree&);
Binarytree& operator = (const Binarytree&);
private:
BinarytreeNode<Ty>* root;
};
int main()
{
char pre[] = {'a','b','d','e','f','g','c'};
char mid[] = {'d','e','b','g','f','a','c'};
std::vector<char> vec_pre(pre, pre+sizeof(pre));
std::vector<char> vec_mid(mid, mid+sizeof(mid));
Binarytree<char, std::vector<char>::iterator>
btree(vec_pre.begin(), vec_pre.end(), vec_mid.begin(), vec_mid.end());
btree.printBinarytree(0/*, std::cout*/);
btree.printBinarytree(1/*, std::cout*/);
std::ostringstream ost;
btree.printBinarytree(2, ost);
std::cout << ost.str();
}output:
abdefgc
debgfac
edgfbca